PARABOLA

 Si un cono es cortado por un plano a través de su eje, y también es cortado por otro plano que corte la base del cono en una línea recta perpendicular a la base del triángulo axial, y si adicionalmente el diámetro de la sección es paralelo a un lado del triángulo axial, entonces cualquier línea recta que se dibuje desde la sección de un cono a su diámetro paralelo a la sección común del plano cortante y una de las bases del cono, será igual en cuadrado al rectángulo contenido por la línea recta cortada por ella en el diámetro que inicia del vértice de la sección y por otra línea recta que está en razón a la línea recta entre el ángulo del cono y el vértice de la sección que el cuadrado en la base del triángulo axial tiene al rectángulo contenido por los dos lados restantes del triángulo. Y tal sección será llamada una parábola , como se puede apreciar en la foto:

Una parábola es el lugar geométrico de los puntos de un plano equidistantes a una recta dada, llamada directriz, y a un punto fijo que se denomina foco.

La longitud del lado recto es siempre 4 veces la distancia focal.

La tangente biseca el ángulo entre el foco, el punto de tangencia y su proyección.

La expresión algebraica que describe una parábola que ocupe cualquier posición en un plano. es:

ax²+bxy+cy²+dx+ey+f=0

si y sólo si:

B²-4ac

y los coeficientes a y c no pueden ser simultáneamente nulos.

ELIPSE

LA ELIPSE ES EL LUGAR GEOMETRICO DE TODOS LOS PUNTOS DE UN PLANO, TALES QUE LA SUMA DE LAS DISTANCIAS A OTROS DOS PUNTOS FIJOS LLAMADOS FOCOS ES CONSTANTE.

UNA ELIPSE ES UN LUGAR GEOMETRICODE TODOS LOS PUNTOS DE UN PLANO PARA LOS CUALES SE CUMPLE QUE EL COCIENTE ENTRE SUS DOS DISTANCIAS A UN PUNTO FIJO, QUE SE DENOMINA FOCO, Y A UNA RECTA DADA, LLAMADA DIRECTRIZ, PERMANECE CONSTANTE Y ES IGUAL A LA EXCENTRICIDAD DE LA MISMA.

ELIPSES SEMEJANTES TEOREMA:

 SI LA INTERSECCION DE UNA RECTACON LA CORONA COMPRENDIDA ENTRE DOS ELIPSES SEMEJANTES CON EL MISMO CENTRO Y EJES CORRESPONDIENTES COLINEALES CONSTA DE DOS SEGMENTOS, ENTONCES ESTOS TIENE IGUAL LONGITUD.

ASINTOTA

En matemática, se le llama asíntota a una línea recta que se aproxima continuamente a otra función o curva; es decir que la distancia entre las dos tiende a cero, a medida que se extienden indefinidamente.
También se puede decir que es la curva la que se aproxima continuamente a la recta; o que ambas presentan un comportamiento asintótico.

en curva polar asintotica

espiral inversa de arquimedes

Asíntota en .

folium de descartes

Asíntota en .

hiperbola vertical (ecuacion resuelta)

Nos dan esta ecuación que corresponde a una sección conica, que corresponde a una hipérbola ya que dado x² y y²son de diferente signo.

9x²-16y²-108x+128y+212=0

9x²-108x-16y²+128y=-212

(9x²-108x)-( 16y²-128y)=-212

Tienes que sacarle mitad al segundo termino de los paréntesis y luego elevar al cuadrado cada uno y poner el resultado de dicha operación sumando al paréntesis que le corresponda y luego multiplicar el numero de afuera por el tercer termino de su paréntesis y sumarlo al resultado:

9(x²-12x)- 16(y²-8y)=-21

9(x²-12x+36)-16(y²-8y+16)=-212+324-256=-144

Factorizamos las dos ecuaciones:

9(x-6)²-16(y-4)²=-144

Luego dividimos entre 144 la ecuación:

9(x-6)²/-144 -16(y-4)²/-144=-144/-144

-(x-6)²/16      +       (y-4)²/9=1

 (y-4)²/9-(x-6)²/16 =1

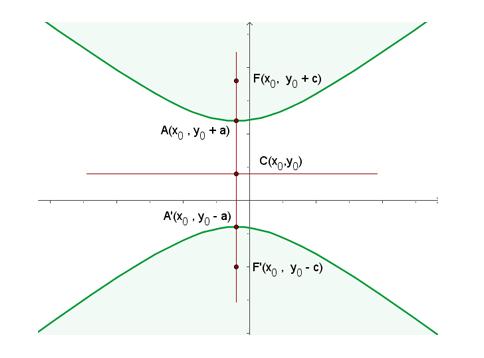
Esto corresponde a una hipérbola vertical y la reconocemos porque el termino positivo lleva la y, con centro (h,k)

Ecuación de una hipérbola con centro en el punto

binomios conjugados(productos notables)

(4a²b+3b²) (4a²b-3b²)=16a ⁴ b²-9b⁴