CÁLCULO DE INTEGRALES DEFINIDAS
Ejercicio 1
Calcule las siguientes integrales definidas:
a)  | b)  | c)  |
d)  | e)  | f) |
g)  | h)  | i)  |
j)  | k)  | l)  |
m)  |
| Respuestas: | a)-2 | b)  | c)  | d)  | e)  | f)  | g) 24,2 | h)  | i) 1 | j)  | k)  | l)  | m) 0 |
Ejercicio 2
Sabiendo que: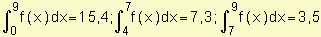 
halle:
halle: a)  | b)  | c)  |
d) | e) | f) |
| Respuestas: | a) 4,6 | b) 10,8 | c) 21,9 | d) 11,95 | e) 3,45 | f) 7 |
Ejercicio 3
a) Calcule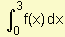 
siendo
.
siendo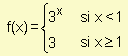. 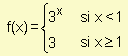b) Encuentre el valor de b tal que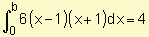 
.
.c) Calcule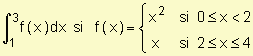
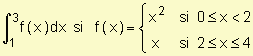
| Respuestas: | a)  | b) b = - 1, b = 2 | c)  |
Ejercicio 4
En la función definida gráficamente por:
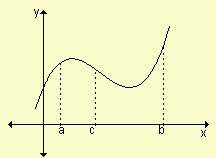
se sabe que 
= 8 y 
= 6. Halle:
= 8 y 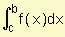= 6. Halle:a)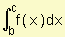 
b) 
e indique qué representa.
e indique qué representa. | Respuestas: a) - 6 b) 2, representa el área de la región entre la gráfica de f, el eje x, las rectas x= a, x= c. |
Ejercicio 5
En la función definida gráficamente por:
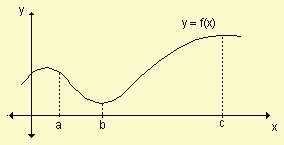
se sabe que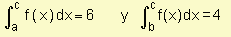 
. Halle:
. Halle:a) 
e indique qué representa
e indique qué representa b)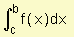
| Respuestas: | a)  e indica el área de la zona entre la gráfica de f, el eje x, las rectas x = a y x = b.b)  = - 4. |
CÁLCULO DE ÁREAS
Se incluyen aquí los ejercicios para calcular áreas y sus respuestas
Ejercicio 6
Escriba, sin calcular, una integral definida que indique el área de la región sombreada.
a)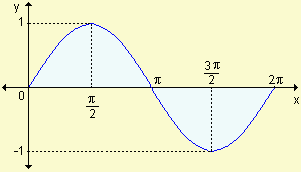 | b) |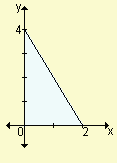
c) 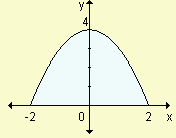 | d)  |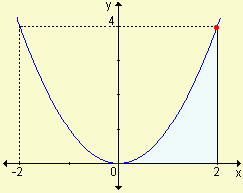
| Respuestas: | a)  | b) |
c) | d) | |
Ejercicio 7
En los siguientes gráficos determine el valor del área sombreada:
a)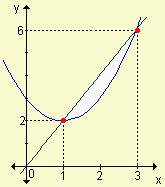 | b)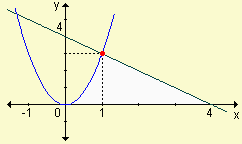 | c) |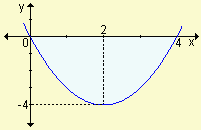
| Respuestas: | a)  | b)  | c) |
Ejercicio 8
Dada la siguiente gráfica
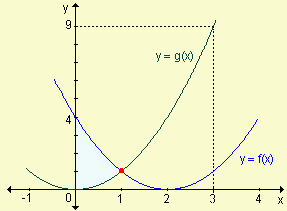
halle:
a) las ecuaciones de las curvas,
b) el área de la zona sombreada.
| Respuestas: | a) y = x2 , y = (x - 2)2 | b) 10 |
Ejercicio 9
Grafique la región limitada por las curvas y calcule el área determinada por ambas.
a) y = x2 con la recta y = 2x + 3
b) el eje de abscisas, la recta y = x + 1 y la recta x = 4
c) el eje de abscisas, la curva y = x2 - 1 y la recta x = 2
d) y = x2 + 2x - 1 con la recta y = - x - 1
e) y2 = 4x con la recta y = 2x - 4
f) y = lnx, el eje de abscisas y las rectas x = 2, x = 10
g) y = x2 con la recta y = 3 - 2x
h) 
con y = x2
con y = x2 i) y = 4 - x2 con la recta y = x + 2
| Respuestas: | a) | b)  | c) | d)  | e) 9 | f) 13,64 | g) | h)  | i) |
Ejercicio 10
Halle el área limitada por la parábola y = 6 + 4x - x2 y el segmento determinado por los puntos A(- 2, - 6) y B(4, 6).
| Respuesta: 36 |
Ejercicio 11
Determine el área sombreada en las siguientes gráficas:
a) 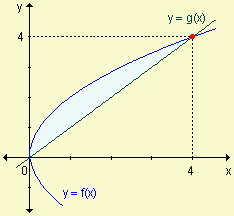 | b) |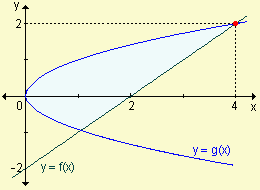
| Respuestas: | a)  b) |
Ejercicio 12
Halle el área encerrada por las curvas y = x2 - 4x e y = 6x - x2 . Grafique.
| Respuesta: | el área vale   |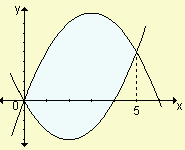
Ejercicio 13
Dada la siguiente gráfica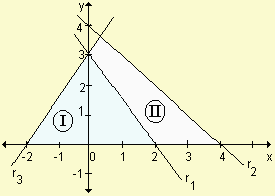 
halle:
halle: a) las ecuaciones de las rectas
b) el área de las zonas I y II indicadas en el gráfico.
| Respuesta: | a)  | b) AI= 6 AII =  |
Ejercicio 14
a) Calcule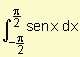 
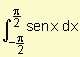
b) Determine el área de la región comprendida entre la curva y = sen x, el eje x y las rectas 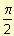x = -
y x = 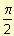. Grafique.
y x = . Grafique. c) Analice por qué no se obtiene el mismo resultado en a) y b).
| Respuesta: | a) 0 b) el área vale 2 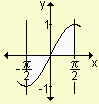 | c) No se puede calcular el área como la integral planteada en (a) ya que da 0 pues las dos tienen el mismo valor absoluto pero distinto signo,geométricamente la región consta de dos partes simétricas respecto del eje x. |
Ejercicio 15
Calcule el área bajo la curva f(x)=
desde 0 hasta 3. Interprete gráficamente. | Respuesta: | el área vale   |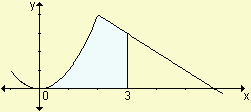
Ejercicio 16
Escriba la integral definida que proporciona el área de la región (no calcule el valor del área)
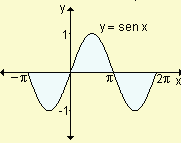
| Respuesta: | A =  |
Ejercicio 17
Halle el área limitada por la parábola y = x2 - x y la recta que une los puntos P(1, 2) y Q(- 3, - 6). Grafique.
| Respuesta: |   |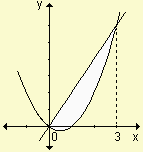
Ejercicio 18
Halle, utilizando integrales, el área del triángulo limitado por las rectas de ecuación y - 3x = 0; x - 3y = 0 y x + y = 4.
| Respuesta: | el área vale 4 |
Ejercicio 19
Calcule el área de la zona limitada por la curva y = x3 - 3x2 - x + 3 y el eje de abscisas.
| Respuesta: | el área vale 8 |
Ejercicio 20
 |  |  |
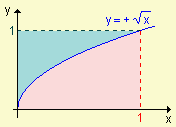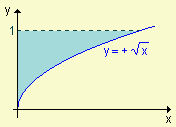